Lecturer: Jason Miller
Contact: jpmiller@statslab.cam.ac.uk
Lecture notes (Last updated: March 11, 2020)
Announcements
- Examples classes will be held in MR11.
- Class 1: Thursday, February 13 at 2:00 pm
- Class 2: Thursday, March 5 at 2:00 pm
- Class 3: Thursday, April 23 at 2:00 pm.
Example sheets
- Example Sheet 1 (Last updated: Feburary 4, 2020. No further questions will be added.)
- Example Sheet 2 (Last updated: February 26, 2020. No further questions will be added.)
- Example Sheet 3 (Last updated: March 4, 2020. No further questions will be added.)
Lecture plan
- Lecture 1: Introduction, plane trees, contour functions
- Lecture 2: The Brownian excursion, real trees
- Lecture 3: The continuum random tree, Gromov-Hausdorff distance
- Lecture 4: Convergence of discrete trees to the continuum random tree
- Lecture 5: Planar maps, the Cori-Vauquelin-Schaeffer (CVS) bijection
- Lecture 6: The CVS bijection continued
- Lecture 7: The Brownian snake
- Lecture 8: Convergence of labelled trees to the Brownian snake
- Lecture 9: Conformal mapping review
- Lecture 10: Half-plane capacity
- Lecture 11: Loewner's theorem
- Lecture 12: Derivation of SLE, phases of SLE
- Lecture 13: Phases of SLE continued
- Lecture 14: Phases of SLE continued
- Lecture 15: Locality of SLE(6)
- Lecture 16: Locality of SLE(6)
References
- G. Miermont. Aspects of random maps
- W. Werner. Random planar curves and Schramm-Loewner evolutions
- G.F. Lawler. Conformally invariant processes in the plane
Links
- Igor Kortchemski's website (simulations of random trees)
- Jeremie Bettinelli's website (simulations of random planar maps) Oded Schramm
- Wendelin Werner and Greg Lawler
- Schramm-Loewner evolution
- Loewner's differential equation
- Loop-erased random walk and percolation theory
- de Brange's theorem (the Bieberbach conjecture)
- Paul Flory and the self-avoiding walk
- Gaussian free field
Notes from related courses
- Stochastic calculus lecture notes due to M. Tehranchi, N. Berestycki , and myself
- Advanced probability lecture notes due to J. Norris and P. Sousi

An embedding into the plane of the continuum random tree (due to Igor Kortchemski)
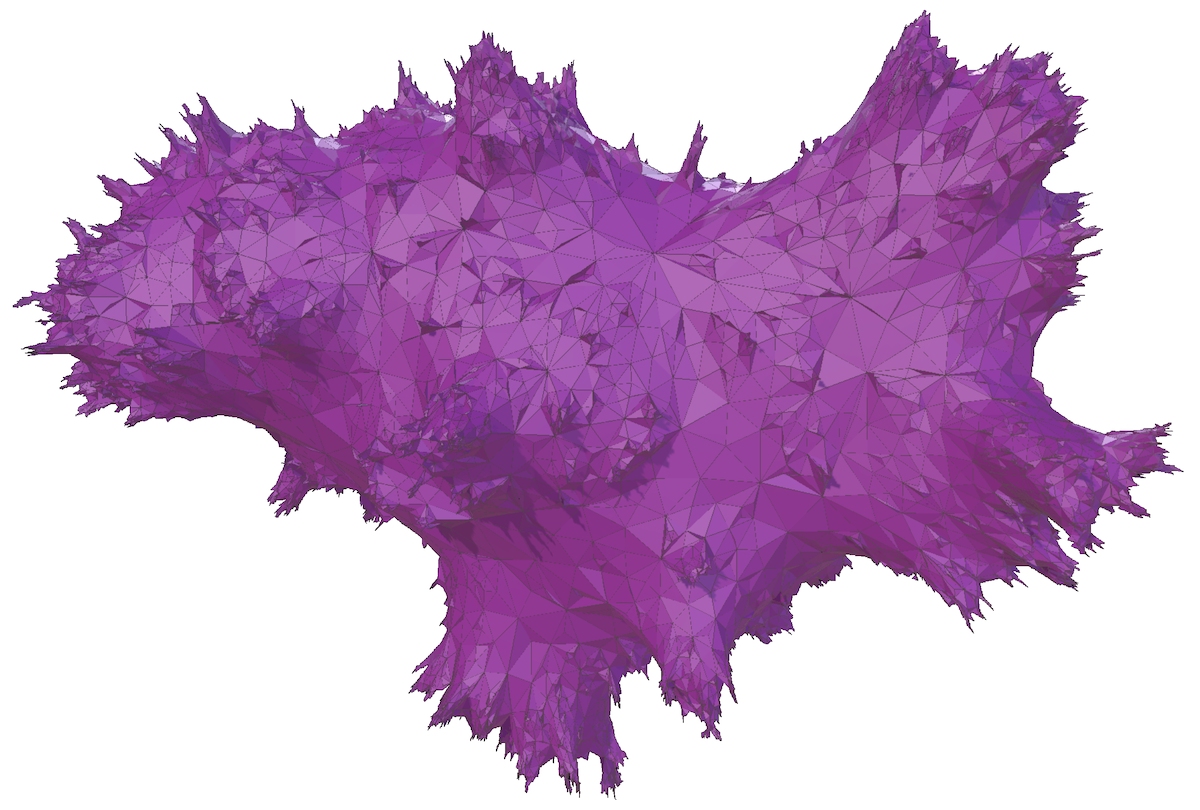
An embedding into R^3 of a random planar map (due to Jeremie Bettinelli)

An SLE(128) curve in the square [-1,1]^2 from i to -i.