I am a professor in the Statistics Laboratory at the University of Cambridge. I am also a fellow of Trinity College. I held the Poincare chair at IHP in the 2015-2016 academic year. Previously, I was a post-doc in the Theory Group at Microsoft Research and at MIT. My research interests are in probability, in particular stochastic interface models (random surfaces and SLE), random walk, mixing times for Markov chains, and interacting particle systems.
A journalistic account in Quanta Magazine of recent work on random geometry with S. Sheffield. My Google scholar profile.
Advances in Asymptotic Probability, in honor of Amir Dembo's 60th birthday.
Scaling limits: from statistical mechanics to manifolds, in honor of James Norris' 60th birthday
Teaching
Lent 2020: Random planar geometry
Lent 2019: Schramm-Loewner evolutions
Lent 2018: Schramm-Loewner evolutions
Lent 2017: Schramm-Loewner evolutions
Michaelmas 2016: Probability and Measure
Lent 2016: Stochastic calculus
Michaelmas 2015: Probability and Measure
Fall of 2014: MIT Math 18.177, a topics course in random planar maps, Liouville quantum gravity, and SLE.
Recent articles
Liuoville quantum gravity metric for gamma in (0,2)
- Local metrics of the Gaussian free field (with E. Gwynne)
- Confluence of geodesics in Liouville quantum gravity for gamma in (0,2) (with E. Gwynne)
- Existence and uniqueness of the Liouville quantum gravity metric for gamma in (0,2) (with E. Gwynne)
- Conformal covariance of the Liouville quantum gravity metric for gamma in (0,2) (with E. Gwynne)
- Equivalence of metric gluing and conformal welding in gamma-Liouville quantum gravity for gamma in (0,2) (with L. Hughes)
Random walk on random planar maps
- Random walk on random planar maps: spectral dimension, resistance, and displacement (with E. Gwynne)
- Harmonic functions on mated-CRT maps (with E. Gwynne and S. Sheffield)
Embeddings of random planar maps
- The Tutte embedding of the Poisson-Voronoi tessellation of the Brownian disk converges to sqrt(8/3)-Liouville quantum gravity (with E. Gwynne and S. Sheffield)
- The Tutte embedding of the mated-CRT map converges to Liouville quantum gravity (with E. Gwynne and S. Sheffield)
- An invariance principle for ergodic scale-free random environments (with E. Gwynne and S. Sheffield)
Percolation on random quadrangulations
- Convergence of percolation on uniform quadrangulations with boundary to SLE(6) on sqrt(8/3)-Liouville quantum gravity (with E. Gwynne)
- Characterizations of SLE(κ) for κ in (4,8) on Liouville quantum gravity (with E. Gwynne)
- Convergence of the free Boltzmann quadrangulation with simple boundary to the Brownian disk (with E. Gwynne)
- Chordal SLE(6) explorations of a quantum disk (with E. Gwynne)
Self-avoiding walk on random quadrangulations
- Convergence of the self-avoiding walk on random quadrangulations to SLE(8/3) on sqrt(8/3)-Liouville quantum gravity (with E. Gwynne)
- Metric gluings of Brownian and sqrt(8/3)-Liouville quantum gravity surfaces (with E. Gwynne)
- Scaling limit of the uniform infinite half-plane quadrangulation in the Gromov-Hausdorff-Prokhorov-uniform topology (with E. Gwynne)
Quantum Loewner Evolution and the Brownian map
- Quantum Loewner Evolution (with S. Sheffield)
- An axiomatic characterization of the Brownian map (with S. Sheffield)
- Liouville quantum gravity and the Brownian map I: the QLE(8/3,0) metric (with S. Sheffield)
- Liouville quantum gravity and the Brownian map II: geodesics and continuity of the embedding (with S. Sheffield)
- Liouville quantum gravity and the Brownian map III: the conformal structure is determined (with S. Sheffield)
Slides on QLE. More slides due to Sheffield from 8-1-2013.
Slides on the equivalence of Liouville quantum gravity and the Brownian map.
Related animations:
Eden model: Animation 1. Animation 2.
Quantum DLA: 0.0 0.25 0.5 0.75 1.0 1.25 1.50 1.75 2.0
(Use VLC to play an MKV file)
Mating of Trees / Peanosphere
- Liouville quantum gravity as a mating of trees (with B. Duplantier and S. Sheffield)
- Liouville quantum gravity spheres as matings of finite diameter trees (with S. Sheffield)
- Brownian motion correlation in the peanosphere for k > 8 (with E. Gwynne, N. Holden, and X. Sun)
- Bipolar oriented random planar maps and SLE_12 (with R. Kenyon, S. Sheffield, and D.B. Wilson)
- An almost sure KPZ relation for SLE and Brownian motion (with E. Gwynne and N. Holden)
- Active spanning trees with bending energy on planar maps and SLE-decorated Liouville quantum gravity for k >8 (with E. Gwynne, A. Kassel, and D.B. Wilson)
- Bipolar oriented random planar maps with large faces and exotic SLE_kappa(rho) processes (with K. Kavvadias)
Slides on the mating of trees
Imaginary Geometry
- Imaginary Geometry I: Interacting SLEs (with S. Sheffield)
- Imaginary geometry II: reversibility of SLE_k(rho_1;rho_2) for k in (0,4) (with S. Sheffield)
- Imaginary geometry III: reversibility of SLE_k for k in (4,8) (with S. Sheffield)
- Imaginary geometry IV: interior flow lines, whole plane reversibility, and space filling paths (with S. Sheffield)
Slides on Imaginary Geometry
SLE and CLE
- Hausdorff dimension of the CLE gasket (with N. Sun and D.B. Wilson)
- Intersections of SLE paths: the double and cut point dimension of SLE (with H. Wu)
- Extreme nesting in the conformal loop ensemble (with S.S. Watson and D.B. Wilson)
- The conformal loop ensemble nesting field (with S.S. Watson and D.B. Wilson)
- Almost sure multifractal spectrum of SLE (with E. Gwynne and X. Sun)
- CLE percolations (with S. Sheffield and W. Werner)
- Dimension transformation formula for conformal maps into the complement of an SLE curve (with E. Gwynne and N. Holden)
- The six-vertex model and Schramm-Loewner evolution (with R. Kenyon, S. Sheffield, and D.B. Wilson)
- Gaussian free field light cones and SLE_kappa(rho) (with S. Sheffield)
- Dimension of the SLE light cone, the SLE fan, and SLE_k(rho) for k in (0,4) and rho in [k/2-4,-2)
- Non-simple SLE curves are not determined by their range (with S. Sheffield and W. Werner)
- Connection probabilities for conformal loop ensembles (with W. Werner)
- Uniqueness of the welding problem for SLE and Liouville quantum gravity (with O. McEnteggart and W. Qian)
- Conformal invariance of whole-plane CLE(kappa) on the Riemann sphere for kappa in (4,8) (with E. Gwynne and W. Qian)
- The geodesics in Liouville quantum gravity are not Schramm-Loewner evolutions (with W. Qian)
- Simple conformal loop ensembles on Liouville quantum gravity (with S. Sheffield and W. Werner)
- Non-simple conformal loop ensembles on Liouville quantum gravity and the law of CLE percolation interfaces (with S. Sheffield and W. Werner)
- Regularity of the SLE(4) uniformizing map and the SLE(8) trace (with K. Kavvadias and L. Schoug)
- CLE(4) and the Gaussian free field (with S. Sheffield)
- Tightness of the chemical distance metric for simple conformal loop ensembles
- Existence and uniqueness of the conformally covariant volume measure on conformal loop ensembles (with L. Schoug)
- A continuous proof of the existence of the SLE(8) curve (with V. Ambrosio)
- Conformal removability of SLE(4) (with K. Kavvadias and L. Schoug)
- Conformal removability of non-simple Schramm-Loewner evolutions (with K. Kavvadias and L. Schoug)
Random walk


A space-filling SLE(6) from the top to the bottom of the square, generated using the Gaussian free field. Animation.
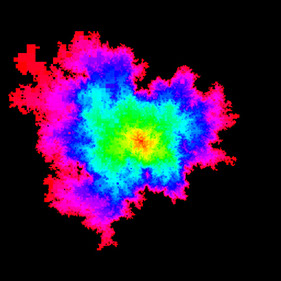
Eden model on a discretization of a pure Liouville quantum gravity surface. This is a discrete analog of QLE(8/3,0). Animation 1. Animation 2.

Tutte embedding of a mated-CRT map with 2,500,000 vertices. Larger size. More images.

Tutte embedding of a mated-CRT map with 2,500,000 vertices. Larger size. More images.

Circle packing of a tree-weighted random planar map generated using the Hamburger-Cheeseburger bijection and Ken Stephenson's software CirclePack. Animation. Larger size.

Percolation interfaces between critical bond percolation clusters. Larger size.